Benchmarks
Benchmarks
SuchTree is motivated by the observation that the memory usage of distance
matrixes grows quadratically with taxa, while for trees it grows linearly.
A matrix of 100,000 taxa is quite bulky, but the tree it represents can be made
to fit into about 7.6MB of RAM if implemented using only C primitives. This
is small enough to fit into L2 cache on many modern microprocessors. This comes
at the cost of traversing the tree for every calculation (about 16 hops from
leaf to root for a 100,000 taxa tree), but, as these operations all happen
on-chip, the processor can take full advantage of
pipelining,
speculative execution
and other optimizations available in modern CPUs. And, because SuchTree objects
are immutable, they are thread-safe. You can take full advantage of modern
multicore chips.
Here, we use SuchTree to compare the topology of two trees built
from the same 54,327 sequences using two methods : neighbor joining
and Morgan Price's FastTree
approximate maximum likelihood algorithm. Using one million randomly
chosen pairs of leaf nodes, we look at the patristic distances in each
of the two trees, plot them against one another, and compute
correlation coefficients.
On an Intel i7-3770S, SuchTree completes the two million distance
calculations in a little more than ten seconds.
from SuchTree import SuchTree
import random
T1 = SuchTree( 'data/bigtrees/ml.tree' )
T2 = SuchTree( 'data/bigtrees/nj.tree' )
print( 'nodes : %d, leafs : %d' % ( T1.length, len(T1.leafs) ) )
print( 'nodes : %d, leafs : %d' % ( T2.length, len(T2.leafs) ) )
nodes : 108653, leafs : 54327
nodes : 108653, leafs : 54327
N = 1000000
v = list( T1.leafs.keys() )
pairs = []
for i in range(N) :
pairs.append( ( random.choice( v ), random.choice( v ) ) )
%time D1 = T1.distances_by_name( pairs ); D2 = T2.distances_by_name( pairs )
CPU times: user 10.1 s, sys: 0 ns, total: 10.1 s
Wall time: 10.1 s
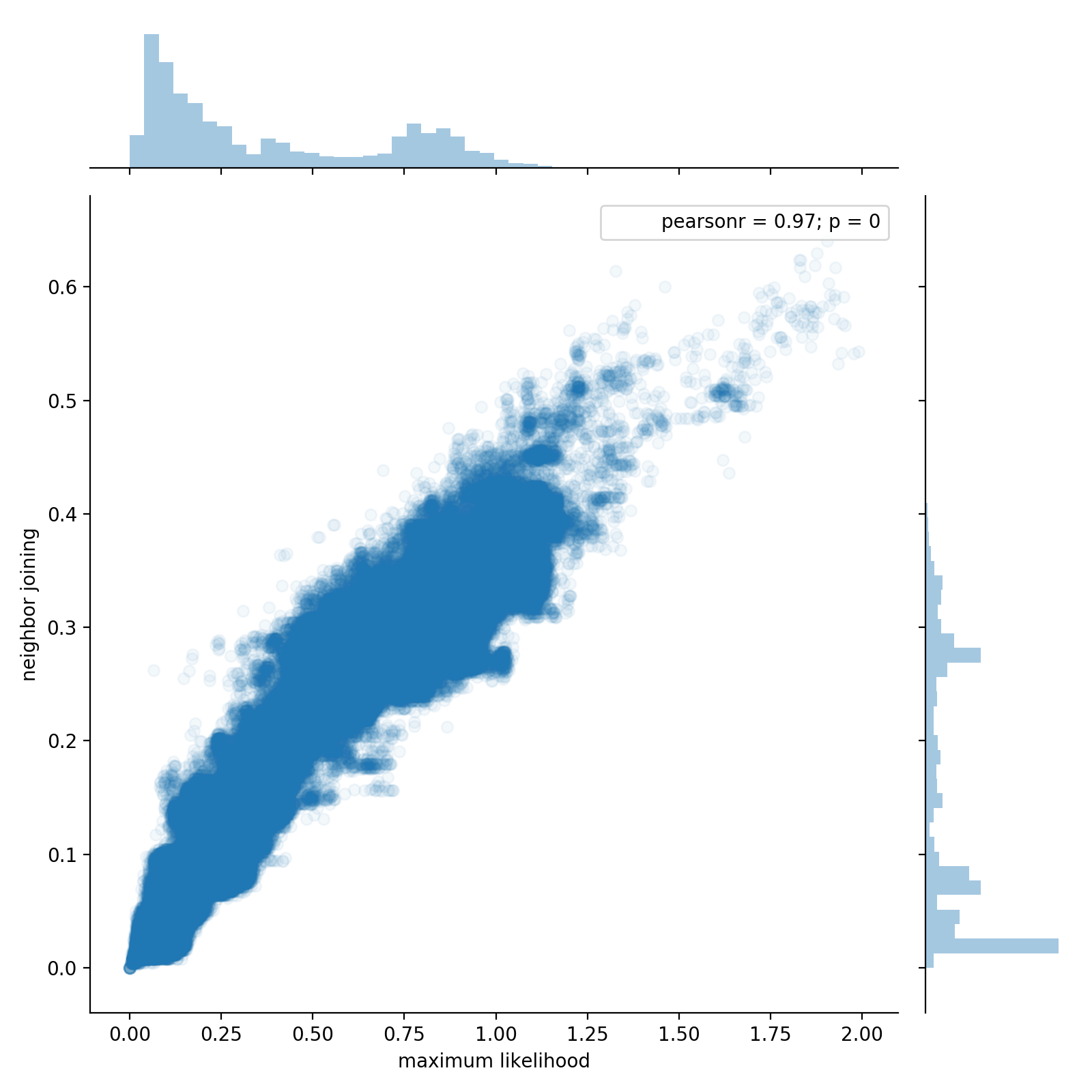
from scipy.stats import kendalltau, pearsonr
print( 'Kendall\'s tau : %0.3f' % kendalltau( D1, D2 )[0] )
print( 'Pearson\'s r : %0.3f' % pearsonr( D1, D2 )[0] )
Kendall's tau : 0.709
Pearson's r : 0.969